9.36减1.76目录
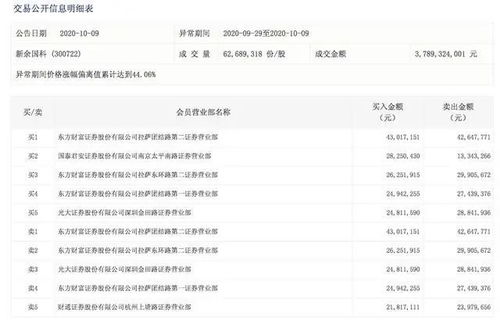
9.36减1.76的结果是7.6[][][]。 1.加法结合律 2.加法交换律 3.乘法结合律 4.乘法交换律 5.乘法分配率 (还有除法的基本性质,不知算不算是) 小弟经验不足,答案仅供参考 例11.24 0.78 8.76 解原式=(1.24 8.76) 0.78 =10 0.78 =10.78 解题关键和提示 运用加法的交换律与结合律,因为1.24与8.76结合起来,和正好是整数10。 例2933-157-43 解原式=933-(157 43)=933-200=733 解题关键和提示 根据减法去括号的性质,从一个数里连续减去几个数,可以减去这几个数的和。 因此题157与43的和正好是200。 例34821-998 =4821-1000 2=3823 解题关键和提示 此题中的减数998接近1000,我们就把它变成1000-2,根据减法去括号性质,原式=4821-1000 2,这样就可口算出来了,计算熟练后,998变成1000-2这一步可省略。 例40.4×125×25×0.8 解原式=(0.4×25)×(125×0.8)=10×100=1000 解题关键和提示 运用乘法的交换律和结合律,因为0.4×25正好得10,而125×0.8正好得100。 例51.25×(8 10) 解原式=1.25×8 1.25×10=10 12.5=22.5 解题关键和提示 根据乘法分配律,两个加数的和与一个数相乘,可用每一个加数分别与这个数相乘,再把所得的积相加。 例69123-(123 8.8) 解原式=9123-123-8.8=9000-8.8=8991.2 解题关键和提示 根据减法去括号的性质,从一个数里减去几个数的和,可以连续减去这几个数,因为9123减去123正好得9000,需要注意的是减法去掉括号后,原来加上8.8现已变成减去8.8了。 例71.24×8.3 8.3×1.76 解原式=8.3×(1.24 1.76)=8.3×3=24.9 解题关键和提示 此种解法是乘法分配律的逆运用。 即几个数同乘以一个数的和,可用这几个数的和乘以这个数。 例89999×1001 解原式=9999×(1000 1)=9999×1000 9999×1 =10008999 解题关键和提示 此题把1001看成1000 1,然后根据乘法的分配律去简算。 例932×125×25 解原式=4×8×125×25 =(4×25)×(8×125) =100×1000 =100000 解题关键和提示 把32分解成4×8,这样125×8和25×4都可得到整百、整千的数。 0.4×125×25×0.8 =(0.4×25)×(125×0.8) =10×100=1000 1.25×(8 10) =1.25×8 1.25×10 =10 12.5=22.5 9123-(123 8.8) =9123-123-8.8 =9000-8.8 =8991.2 1.24×8.3 8.3×1.76 =8.3×(1.24 1.76) =8.3×3=24.9 9999×1001 =9999×(1000 1) =9999×1000 9999×1 =10008999 14.8×6.3-6.3×6.5 8.3×3.7 =(14.8-6.5)×6.3 8.3×3.7 =8.3×6.3 8.3×3.7 8.3×(6.3 3.7) =8.3×10 =83 1.24 0.78 8.76 =(1.24 8.76) 0.78 =10 0.78 =10.78 933-157-43 =933-(157 43) =933-200 =733 4821-998 =4821-1000 2 =3823 I32×125×25 =4×8×125×25 =(4×25)×(8×125) =100×1000 =100000 9048÷268 =(2600 2600 2600 1248)÷26 =2600÷26 2600÷26 2600÷26 1248÷269 =100 100 100 48 =348