1.80除32目录
这是序言。
在数学中,除法是基本的计算过程,可以帮助解决很多实际问题。今天讨论具体的除法问题。1.80除以32。这个问题虽然简单,但是通过解答它可以加深对除法概念的理解。
。
。
问题分析。
在开始计算之前,有必要明确几个要点。1.80是小数,32是整数。在进行除法的时候,小数和整数的除法规则是不同的。你需要确定计算结果是小数还是整数。
。
。
计算步骤。
计算1.80除以32时,需要如下步骤。
。
。
把1.80转换成分数。1.80是180/100,所以1.80可以用分数180/100来表示。
分数180/100除以32。除法可以转换为乘法,即a/b÷c=a/b×1/c,所以问题可以转换为180/100×1/32。
计算乘法。分子相乘为180×1=180,分母相乘为100×32=3200。结果是180/3200。
简化分数。为了简化分数,我们需要找到分子和分母的最大公约数。180和3200的最大公约数是40。所以分数180/3200可以简化为9/160。
把分数转换成小数。分子9除以分母160,得到0.05625。
。
。
分析结果。
根据以上的计算,1.80除以32就是0.05625。这个结果是小数,1.80是32的0.05625倍。在日常生活中,我们可以利用这个结果估算出1.80和32的比例关系。
。
。
并投入使用。
在实际生活中,除法被广泛使用。以下是1.80除以32的现实情况。
。
。
假设有一块长1.80米、宽0.5米的长方形木板。如果要将其切割成宽0.05625米的木板,需要切割32次。
如果你有一瓶1.80升的饮料,你想把它均分到32瓶0.05625升的饮料中,那么你可以在每瓶饮料中放入0.05625升的饮料。
按建筑设计计算,长1.80米、宽0.5米的长方形面积为0.9平方米。把这个面积平均分配到32个区域,每个区域的面积是0.028125平方米。
。
。
通过解答32除1.80的问题,不仅加深了对除法概念的理解,还了解了除法在实际生活中的应用。在数学的学习中,注重理论联系实际,帮助解决实际问题。
。
。
数学运算小数除法实际应用分数化的简单分数。

31.8除以2.5的竖式计算方法详解
在数学的学习中,小数的除法是基础和重要的部分。本文将详细介绍1.8除以2.5的纵式计算方法,帮助大家理解和掌握小数除法。
3
标记:小数除法,竖式计算,数学基础
3
准备阶段:理解纵向计算的基础
在进行竖式计算之前,首先有必要了解竖式计算的基本知识。所谓竖式计算,是指将数字按照一定的形式排列,然后逐一除法得到结果的方法。小数的除法需要注意以下几点。
小数点对齐:在纵向计算中,被除数和除数的小数点必须对齐。
逐位除法:从被除数的最高位开始逐位除法。
商的决定:各位商需要根据被除数和除数的实际值来决定。
3
标记:竖式计算原则,小数点对齐,每一位除法
3
1.8除以2.5的竖式计算。
这里,纵向计算1?8除2?以第5项为例进行说明。
1?8和2?把5竖着排列,小数点对齐。
因为2.5不能整除1.8,所以在1.8后面加0,得到18,再做除法。
开始逐位除法。18除以2得到9。把9写在商的第一位。
然后用9乘以2.5得到22.5。把22.5写在18的下面,做减法得到5.5。
因为5.5小于2.5,所以不能除法,所以1.8除以2.5就是0.72。
3
标签:计算步骤,逐位进行除法、减法运算。
3
来确认计算结果的正确性。
竖式的计算结束后,为了确认准确性要进行验算。验算的方法是把商乘以除数,看是否等于被除数。
商0.72除以2.5,得到1.8。
1.8是被除数,所以计算是正确的。
3
标记:检验过程,乘法,正确性。
3
1.8除以2.5的纵式计算方法。
这样就可以得到1.8除2.5的纵向计算。在进行小数除法的纵向划分时,有几点需要注意。
把小数点对齐。
逐位除法,从被除数的最高位开始。
各位商,需要根据被除数和除数的实际值来决定。
计算结束后,进行验算,确保确定性。
3
标记:小数点对齐,验算
3
扩展:小数除法的应用。
小数除法在日常生活和工作中被广泛使用。比如计算商品价格、计算投资回报率、解决实际问题等。通过掌握小数除法的竖式计算法,就能应对各种各样的数学问题。
3
标签:应用,日常生活,实际问题
到此为止详细说明了,1?把8变成2?想必大家已经知道了除以5的纵向计算方法。希望大家在今后的学习和工作中,也能灵活运用这个方法来解决数学问题。
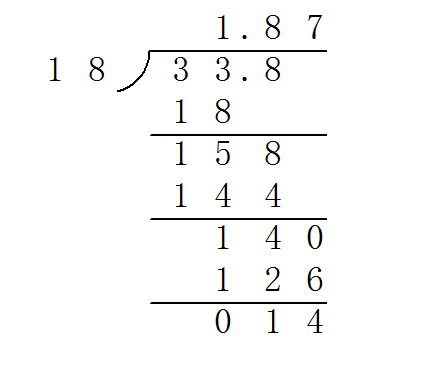
3引言
在数学的学习中,小数的除法是基础和重要的部分。本文将详细介绍使用竖式计算3.38除以1.8的解题方法,并说明计算步骤和注意事项。
3
准备阶段。
在纵向计算之前,有必要确认被除数和除数是否都是整数。在3.38除以1.8的问题中,将小数点向右移动一位,就可以将两者都转换为整数。具体如下。
被除数3.38等于33.8。
除数1.8等于18。
3
纵向计算的步骤。
这里已经简化为33.8除以18的问题,我们可以试着用竖式进行计算。
把除数18写在竖的左侧,把33.8写在竖的右侧。
从被除数的最高位开始,即从左到右,逐位进行除法。
看33能不能被18整除。33比18小,所以我们需要考虑下一位38。
38除以18,等于2余数2。竖的下面写2,余数的2和下一位的8组合起来就是28。
二十八除以十八,就是一余数的十。在竖型下面写1,余数的10和下一位的0组合起来就是100。
一百除以十八,就是五余数的十。竖型的下面写5,余数的10和下一位的0组合起来就是100。
重复上述步骤,直到余数小于除数。
3
计算结果。
这样就可以计算出3.38除以1.8。下面是垂直计算的完整过程。
```
吗?1.8|33.8
????是-18。
????----
????15
????-14.4。
????----
????1.6。
????-1.8。
????----
????0.8。
????-0.72。
????----
?????08
????负0.072。
????----
????0.008。
????-0.006。
????----
?????是002
```
最终,得到了1.877777的商…这是循环小数,循环节是7。
3
循环小数的表达。
在数学中,循环小数可以用几种方法来表示。关于1.877777…这个循环小数可以表示为:
1.877(7)。
1.87(7)。
1.878…
这里,括号表示循环节的开始和结束,省略号表示循环节的继续。
3
总结一下
通过这篇文章,我们知道了使用竖式计算3.38除以1.8的解题方法。在计算过程中,要注意小数点的位置和位数的对齐,以确保计算的准确性。同时,我们也学习了循环小数的表示方法,这对于理解和应用小数的除法运算有重要的意义。
3
标签。
3引言 除法是数学世界中理解数值关系的基本计算方法。今天给大家介绍一个简单的除法问题32除8是多少看似简单的问题,却能帮助大家更好地理解除法的概念和应用。 3 基本的概念。 在数学中,除法是分配或分割的过程。“32除以8”是指将32个单位平均分成8等份,得到多少。这个问题的答案是4。因为4乘8等于32。 3 计算过程。 计算32除8时,可以使用长除法,也可以直接使用计算器。接下来是使用长除法将32除以8的步骤。 把32写在长除法的左侧,把8写在长除法的右侧。 8除以32的第一个数字3就是0。因为8不能整除3。 8除以32的前两位数32就是4。因为8乘4等于32。 在长除法上画4,再减去32,然后32乘以4(即128),得到的就是0。 因为余数是0,所以32除以8得到的商是4。 3 除法的应用。 除法在日常生活中被广泛使用。例如,如果你想把32个苹果均分给8个朋友,你可以使用除法计算每个人能得到多少个苹果。同样,如果你想知道汽车以每小时32公里的速度行驶8个小时会增加多少距离,你也可以用除法计算。 3 除法的性质。 除法有以下重要的性质。 商的性质:用一个数除以另一个数,再用除数乘以商,就得到原来的被除数。 除法的反算:乘法是除法的反算。例如,32除以8等于4,那么8乘以4也是32。 除法的除法:一个数除以和的时候,这个数除以各个加数就能相加。 3 除法和其他运算的关系。 除法和其他数学有密切的关系。例如,使用除法,求百分比,比率,分数。除法是解决方程式和几何计算等很多数学问题的基础。 3 除法的扩展。 在更高级的数学中,除法可以扩展到复数和实数。通过这些扩展,除法在解决更复杂的问题时变得有用。例如,在工程学和物理学中,经常会涉及复数和实数除法的问题。 3 结论。 32除8等于4。这是一道简单的除法题,通过对它的分析,可以帮助我们更好地理解除法的基本概念、性质和应用。无论是日常生活,还是更复杂的数学问题,除法都是重要的工具。掌握除法可以帮助你更好地理解数学的世界,在各种情况下做出明智的决定。 3 标签:除法数学运算32除法8长除法扩展应用性质
