标准正态分布1.76目录
标准正态分布的概况。
标准正态分布也被称为标准正态分布(StandardNormalDistribution),是平均值为0,标准差为1的特别正态分布。标准正态分布在统计学和概率论中是一个非常重要的概念,它为数据标准化提供了基础,可以对不同分布的数据进行比较分析。
。
。
标准正态分布的定义和特征。
标准正态分布的概率密度函数(PDF)可以这样表示:
。
f(x)=\\\\\\\\\\\\\\\\[frac{1}{sqrt2\\\\\\\\\\\\\\\\pi{}}e^{-\\\\\\\\frac{x^2}{2}}\\\\\\\\]。
(x中,\\\\\\\\\\\\\\\\),向量\\\\\\\\\\\\\\\\sqrt(2pi}{\\\\\\\\\\\\\\\\),常数\\\\\\(e\\\\\\)的自然对数,。
。
标准正态分布具有以下性质。
。
。
对称性:标准正态分布以0为中心对称。
平均值和标准差:平均值是0,标准差是1。
68-95-99.7规则:在标准正态分布中,约68的数据点位于平均值加1个标准差的范围内,约95的数据点位于平均值加2个标准差的范围内,约3个标准差的范围内99.7。
。
。
标准正态分布的应用。
标准正态分布广泛应用于各个领域,但也有以下几种常见情况。
。
。
统计学:在假设检验、置信区间估计、回归分析等统计方法中,标准正态分布是重要的参考分布。
工程学:在质量管理、可靠性分析、信号处理等领域,标准正态分布被用于评价系统的性能和可靠性。
医学:在生物统计学、流行病学、临床试验等领域,标准正态分布被用于分析数据、评价治疗效果、预测疾病风险等。
金融:在风险管理、资产定价、资产组合优化等领域,标准正态分布被用于评估金融市场的风险和回报。
。
。
标准正态分布的图。
在Python中,你可以使用matplotlib库创建概率密度曲线(PDF)和累积概率密度函数(CDF)。
。
```是python。
importnumpyasnp。
importmatplotlib.pyplotasplt
。
生成标准正态分布的数据。
x=np。linspace(-4,4,1000)。
pdf=(1/np.sqrt(2np.pi))np.exp(-x2/2)。
cdf=np.cumsum(pdf)。
。
绘制PDF的图表。
plt.figure(figsize=(10,6))。
plt.plot(x,pdf,label='pdf')。
plt.title(标准正态分布概率密度曲线)
plt.xlabel('x')。
plt.ylabel(概率密度)。
plt传奇。
plt.grid(True)。
plt.show。
。
绘制CDF曲线。
plt.figure(figsize=(10,6))。
plt.plot(x,cdf,label='cdf')。
plt.title(标准正态分布的累积概率密度函数)。
plt.xlabel('x')。
plt.ylabel(“累积概率密度”)。
plt传奇。
plt.grid(True)。
plt.show。
```。
。
标准正态分布的Z分数。
标准正态分布的Z分数,也称为标准分数,是将任何正态分布的数据转换成标准正态分布数据的量度方法。Z分数的计算公式如下。
。
\\\\\\\\[Z=frac{x-\\\\\\\\mu}{\\\\\\\\sigma}\\\\\\\\]。
(x中,\\\\\\\\\\\\\\\\)是原始的数据显示,\\\\\\\\\\\\\\\\mu\\\\\\\\()数据均等于\\\\\\\\\\\\\\\\σ\\\\\\\\()数据的标准偏差。
。
通过计算Z得分,可以对分布不同的数据进行比较分析,从而更好地理解数据的分布特征。
。
。
标准正态分布是统计学和概率论中广泛使用的一种特殊正态分布。在这篇文章中,你可以了解标准正态分布的定义,特性,应用和绘制方法。在实际应用中,掌握标准正态分布的相关知识对于数据分析和决策具有重要意义。
。

3如何标准化正态分布——深度解析标准化过程
在统计学和数据分析中,正态分布是表示数据针对某一特征的分布的概率分布。在实际应用中,为了进行更深入的分析和比较,需要将正态分布的数据转换成标准正态分布。本文将对正态分布进行标准化,探讨其背后的原理和应用。
3
标签:正态分布,标准化,统计学
3
一、什么是正态分布
正态分布也被称为高斯分布,是概率密度函数呈对称钟形曲线的连续概率分布。在正态分布中,数据集中在平均值附近,出现偏离平均值的数据的概率会变小。正态分布由平均值(μ)和标准差(σ)两个参数决定。平均值决定分布的中心,标准差决定分布的扁平度。
3
标签:正态分布,平均值,标准差。
3
二、什么是标准正态分布
标准正态分布是平均值为0,标准差为1的特别正态分布。标准正态分布用(0,1)表示。在标准正态分布中,所有数据点都对平均值对称,分布的形状是固定的。标准正态分布在统计学中是非常重要的概念,它可以使数据的分析和比较变得简单。
3
标签:标准正态分布、平均值、标准差。
3
三、正态分布的标准化原理。
正态分布的标准化是指将任意平均值和方差的正态分布转换成平均值为0、标准差为1的正态分布。这个过程可以用以下的公式来执行。
如果X遵循正态分布(μ,σ2),那么其标准化的Z就遵循标准正态分布(0,1)。
公式如下。
Z=(x-μ)/σ。
其中Z是标准化数据,X是原始数据,μ是原始数据的平均值,σ是原始数据的标准差。
3
标签:正态分布,标准正态分布,标准化公式。
3
四、正态分布的标准化步骤
求原始数据的平均值(μ)和标准差(σ)。
2.从每个原始数据点X减去平均值μ。
3.将步骤2得到的结果除以标准差σ。
4.得到标准化数据Z。
3
标签:正态分布,标准正态分布,标准化步骤
3
五、正态分布标准化的应用
正态分布的标准化在统计学和数据分析中被广泛使用,以下是一些常见的应用。
1.数据比较:通过标准化不同数据集的正态分布来进行数据比较?分析变得容易。
2.统计推断:标准正态分布是假说检验和置信区间推断中经常使用的参考分布。
3.机器学习:用机器学习算法标准化正态分布有助于提高模型的性能和稳定性。
3
标签:正态分布,标准正态分布,应用场景。
3
六、总结。
正态分布的标准化指的是将任意平均值和方差的正态分布转换成标准正态分布。标准化可以使数据的分析和比较变得简单,提高统计推理的精度。我详细介绍了正态分布标准化的原理、步骤和应用,希望对读者有所帮助。
3
标签:正态分布,标准正态分布,总结。

3标准正态分布表0.95对应值详解
标准正态分布表是统计学中常用的工具,有助于理解和计算正态分布的概率。本论文将详细说明标准正态分布的0.95值,并说明其背后的统计学机制。
3
标签:标准正态分布,概率和统计学。
3
一、标准正态分布的概要。
标准正态分布也被称为高斯分布,是概率密度函数为贝尔曲线的连续概率分布。标准正态分布的平均值是0,标准差是1。这是所有正态分布的特例,也是统计学中最常见的分布之一。
3
标签:高斯分布,平均值,标准差。
3
二、标准正态分布表的作用
标准正态分布表提供了快速找到对应于特定z分数(标准分数)的概率的方法。z得分是以标准差为单位,表示某数据点到平均值的距离。通过寻找标准正态分布表,我们可以找到任意z得分的累积概率。
3
标签:z-score,累积概率,搜索方法
3
三、标准正态分布表中0.95的意义
在正常的正态分布表中,0.95指的是累计概率值。也就是说,从负无限大到z得分的累计概率为0?是95。也就是说,这个z分数对应的概率是0?95,右边的概率是0?是05。
3
标签:累计概率,概率值,0.95。
3
四、找出0.95对应的z分数。
为了找出与标准正态分布0.95相对应的z分数,需要按照以下步骤。
在标准正态分布中找到一列0.95。
接下来,找到一行中最接近0.95的值。通常是0.950。
接下来,我们来看与该数值相对应的z得分值。在标准正态分布表中,0.950对应的z分数约为1.645。
3
标签:查找,z-score,数值对应
3
五、0.95对应z-score的实用化
在统计学中,0?相当于95的z分数(1?645)被广泛使用。例如,假设检验经常使用0.05(α=0.05)的显著性水平。在这种情况下,相当于0.95的z分数(1.645)有助于决定拒绝第一个阈值。
3
标签:假设检验,临界值。
3
六、总结。
标准正态分布表是统计学中不可或缺的工具,可以帮助我们快速调查并计算正态分布的概率。本论文将详细介绍相当于标准正态分布0.95的z分数(1.645),并说明其在统计学中的应用。理解了这些概念,就能更好地利用标准正态分布表来解决实际问题。
3
标签:标准正态分布表,概率计算

3标准正态分布表的调查方法——是实用的指南。
标准正态分布表是统计学中常用的工具,可以帮助我们快速找到特定正态分布的概率值。以下是标准正态分布表使用方法的详细手册。
3
标签:标准正态分布表,概率值,统计学
3
一、了解标准正态分布
标准正态分布也被称为高斯分布,是概率密度函数为贝尔曲线的连续概率分布。标准正态分布的平均值是0,标准差是1。也就是说,所有正态分布都可以通过标准化转换成标准正态分布。
3
标签:标准正态分布,高斯分布,平均标准差。
3
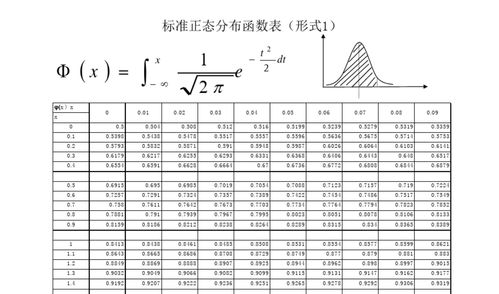
二、标准正态分布表的构成
标准正态分布表通常由z值(标准正态分布的累积概率值)列和对应的概率值列构成。z值是标准正态分布的标准化变量,表示数据点和平均值之间的标准差。
表中的z值按照从小到大的顺序排列,每行表示整数部分,每列表示小数点以下一位数字。例如,z值1.2表示平均值到1.2个标准差之间的位置。
3
标签:标准正态分布表,z值,累积概率值。
3
三、寻找标准正态分布表。
1.确定z值的整数部分和小数部分
确定你想找的z值的整数部分和小数部分。例如,如果z值是1.27,那么整数部分就是1,小数部分就是0.27。
2.找出表格中对应的整数部分。
在表格左侧找到对应z值整数部分的列。例如,针对z值1.27找到列1.2。
3.找到表格中对应的小数。
在表格的顶部,找出z值的小数对应的行。对于1.27的z值,你会发现有一行0.07。
4.读入交叉点的值
在列和行相交的地方,读取对应的值。这个值就是z值所对应的累计概率。例如,z值1.27,而交叉点的值是0.8997。这意味着在标准正态分布中,z值小于1.27的概率是0.8997。
3
标记:查找步骤,整数部分,小数部分,交叉点
3
四、注意事项
1.确认你使用的是标准正态分布表,而不是普通的正态分布表。
2.如果需要寻找z值大于0的概率,请从1中减去z值所对应的累计概率。
3.如果需要寻找两个z值之间的概率,请分别寻找两个z值的累计概率。然后减去。
3
标签:注意事项,正态分布表,累积概率
3
五、总结。
这样一来,使用标准正态分布表查找所需概率值应该就变得简单了。在统计学、工程学、经济学等领域,它是帮助我们快速解决各种概率问题的工具。
3
标签:概率问题,应用领域。
