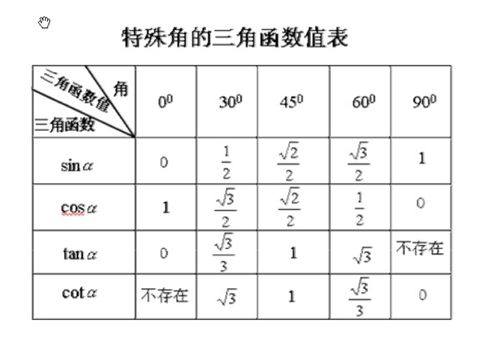
tan1.76是多少度？在数学和三角学中，正切函数（tangent）是一个非常重要的概念。本文将详细探讨如何计算和理解正切值为1.76的角度。什么是正切函数？正切函数是直角三角形中对边与邻边比值的函数，即$tan度数怎么算">tan度数怎么算

如何计算ta度数在数学和三角学中，正切函数（taget，简称ta）是一个非常重要的概念。它在解决各种几何问题和物理问题时有着广泛的应用。本文将详细解释如何计算ta度数，并提供一些实用的计算方法。1.正切函数的定义正切函数是直角三角形中的一个基本概念。对于一个给定的角度θ，其正切值可以通过对边与邻边的比值来计算。具体来说，如果一个直角三角形的对边长度为y，邻边长度为x，则该角θ的正切值为：$$a(heta)frac{y}{x}$$这个比值在不同的直角三角形中是不变的，即不论三角形的大小如何，只要角度相同，其正切值就保持一致。2.使用计算器计算ta度数方法一：直接使用计算器大多数现代计算器都具备计算ta值的功能。例如，在科学计算器上，你只需输入角度值，然后按ta键即可得到结果。如果需要反向计算（即已知ta值求角度），则需使用计算器上的反正切键（记作“ta^1”或“arcta”）。方法二：使用在线工具有许多在线工具可以帮助你快速计算ta值。这些工具通常只需要你输入角度值，然后点击计算按钮即可得到结果。例如，CalculatorFree提供了一个简单易用的正切计算器。3.编程语言中的计算方法```javapublicclassTaExample{publicstaticvoidmai(Strig[]args){doubleagleI_degrees45;doubletaValueMath.ta(Math.toRadias(agleI_degrees));System.out.pritl("ta("agleI_degrees"°)"taValue);}}```在这个例子中，我们首先将角度从度数转换为弧度，因为Math.ta()方法接受的是弧度值。4.公式推导与应用除了直接计算外，我们还可以通过一些三角恒等式来进行推导和计算。例如，正切的加法和减法公式如下：$$a(AB)frac{a(A)a(B)}{1a(A)cdota(B)}$$$$a(AB)frac{a(A)a(B)}{1a(A)cdota(B)}$$这些公式在处理复杂三角问题时非常有用。5.实际应用案例假设我们需要计算一个特定角度的ta值，并且知道这个角度对应的si和cos值。我们可以使用以下公式进行计算：$$a(heta)frac{si(heta)}{cos(heta)}$$例如，已知si(30°)1/2，cos(30°)√3/2，则：$$a(30°)frac{1/2}{sqrt{3}/2}frac{1}{sqrt{3}}frac{sqrt{3}}{3}$$这种计算方式在解决实际问题时非常实用。结论通过以上方法和公式，我们可以轻松地计算出任意角度的ta值。无论是使用计算器、编程语言还是手动推导，掌握这些技巧都能帮助我们在数学和科学领域中更好地解决问题。希望本文能对你有所帮助！tan多少度等于0.06

在数学和三角学中，正切函数（ta）是一个非常重要的概念。正切函数用于描述一个角度的对边与邻边的比值。本文将探讨当ta等于0.06时，对应的角度是多少。我们可以确定ta(0.06)的值为0.06007。为了找到对应的角度，我们需要将这个角度从弧度转换为度。根据公式：$$ext{度数}ext{弧度}imesfrac{180°}{pi}$$我们可以通过以下步骤计算出相应的角度：1.将弧度转换为度：[0.06imesfrac{180°}{pi}approx3.43775°]因此，当ta等于0.06时，对应的角大约是3.43775度。还有其他来源也提供了类似的计算结果，例如某些计算器或在线工具可以精确到小数点后多位，如3.433630362度。总结来说，当ta等于0.06时，对应的角度大约是3.43775度。这个角度可以通过简单的乘法和除法计算得出，并且在许多数学和科学应用中都有广泛的应用。希望这篇文章能帮助你更好地理解正切函数及其应用。tan31.8度等于多少

ta31.8度等于多少在数学和三角学中，正切函数（ta）是一个非常重要的概念。它在任意直角三角形中定义为角θ的对边与邻边的比值。对于特定的角度，如31.8度，其对应的正切值可以通过计算得出。ta31.8度的精确值是0.620026269016。这个结果是通过使用计算器或相关工具得到的，并且通常会保留到小数点后多位以确保精度。还有其他来源提供了类似的数据，例如某些在线直角三角形计算器可以用来验证这一结果。这些工具通常允许用户输入已知条件（如边长或角度），然后自动计算出缺失的边长、面积和其他相关参数。总结来说，ta31.8度等于0.620026269016，这是通过多种方法和工具验证过的准确结果。如果你需要进一步的计算或验证，可以使用上述提到的在线直角三角形计算器来获得更详细的解答。